• Rob Fielding <rob.fielding@gmail.com>
• My Resume
• YouTube
• Random blogposts, mostly iOS, MIDI, and programming
• The Source Code for this site, including the guitar diagram generation
• 8-dot Computer Braille Editor

This is a github and hardware project using an Arduino UNO board (AVR chip, 2k RAM, etc.) to proxy the MIDI protocol to change the capabilities of MIDI controllers like keyboards, in a format that is similar to guitar pedal stompbox devices. The point is in doing these C++ projects that run under very tight size and real-time constraints.

When the iPad first came out, I was doing serious iOS music application development.

• Mugician (source still on my github account in Mugician repo - dozens of clones of it still exist in the app store)
• Geo Synthesizer (a commercial venture with Dream Theater's keyboardist Jordan Rudess, related to upcoming GeoShred app that Wizdom/MoForte is working on at the moment)
• Cantor / AlephOne (a simplified app similar to Geo - source in github under the repo name AlephOne)

When the iPad first came out, there was no MIDI support available, so Mugician had its own sound engine. By contrast, the app featured here was originally written to use MIDI internally, and was originally targeted to only pair with the app ThumbJam, due to the extreme re-interpretation of the MIDI protocol required to do fretless polyphonic instruments correctly.

Into the first year of iPad, the typical iOS music app had far too much latency to be a viable music instrument (music instruments must be in the 10ms of latency range... 1/100 of 1 second touch to audio response; at a time when 100ms was the norm.). Mugician and Geo Synthesizer were widely regarded as some of only a handful of iOS instruments which could be played at the actual speed that real musicians could throw at it. (Much of this was achieved by avoiding UIKit in favor of OpenGLES2 up until the real-time issue became less of a problem.)

In addition to mobile apps, I did some experimentation on Microsoft Windows with large touchscreens, in this case using OSC protocol rather than standard MIDI:

These diagrams give an idea of how quartertone modes work. This is loosely based on Maqam music theory (ie: Arabic/Turkish music). This system has a large variety of scales that are built of smaller chunks, and do not force alternation between major and minor tonalities. The use of quartertones gives a lot more scope for using minor tonalities in more places, along with some neutral ones. The theory I am laying out is however more oriented towards playing heavy metal on a quartertone guitar.

Instruments

• Quartertone Electric - Reasonable approximations to Maqam can be played in a rock/metal context. Pictured is a standard Stratocaster refretted for 24EDO (ie: 24 notes per octave, or doubled fretting).
• Fretless - Harder to fit in with standard instruments, but more true Maqam is playable .
• See Maqam World for a more standard treatment of Maqam, including the microtonal details, and traditional features. What I am documenting is more oriented towards using 24EDO in a heavy metal context.
• The guys that actually built my quartertone guitar: Metatonal Music

Patterns

• keep in mind that fret numbers are double what they are on normal guitar. conveniently, new strings start on multiples of 10, presuming it is tuned to all fourths as here.
• A small tone is the normal half tone in 12ET - 2 frets on quartertone guitar
• A large tone is the normal whole tone in 12ET - 4 frets on quartertone guitar
• A neutral tone is half-way in between small and large - 3 frets on a quartertone guitar.
• It is almost always the case that neutral tones appear next to each other in pairs, such that they span a minor third, and this minor third is on even frets to line up with 12EDO.
• In terms of frets: 0 4 6 is a "Minor" pattern, due to resembling bottom part of a minor scale.
• In terms of frets: 0 2 6 is a "Phrygian" pattern, due to resembling bottom part of a phrygian scale.
• In terms of frets: 0 3 6 is a "Bayati" pattern, due to having two neutral seconds right next to each other.

All of these scale diagrams are JavaScript Canvas code (not static images). Feel free to grab the code out of this page to make microtonal fretboard diagrams, as the code is general enough to do this.

Over Minor Pentatonics

When starting out on the root note (E in this case), if we have a Minor Pentatonic backing scale, then we make it Bayati by adding note 1. Being neither Phrygian (ie: Kurd) nor Minor (ie: Nahawand), choosing Bayati picks note 0 as the clear root. From note 0 to note 2, a minor third is being cut exactly in half; something impossible on a 12EDO instrument. It has two medium second intervals next to each other, noted as "MM":

Compare with Minor

Compare with Phrygian

As chord progressions change, the bottom half of the scales (tetrachords) define the notes in use. Usually the scale isn't defined rigidly across the entire octave. The idea is to string together shorter partial scales. In this way, many melodic runs will be full of accidentals, while still having a clear tonal character.

Modulating

As we move up, we can either do Phrygian on B, or use Bayati on B. In this position, Bayati is picked. Note that it exhibits some symmetry with Bayati on E from notes 3 through 5. Note 4 is a quartertone flat from being a fifth above B (an F♯), so it is clearly connected to E.

Minor

When modulating down to A, we pick the minor shaped scale. Because we are connecting to adjacent scales like Bayati on E and B, we probably want to preserve the B. It has large then small intervals, noted as "LS":

Similarly, when modulating down to D, we pick the minor shaped scale. Because we want to preserve our minor third, we can make F natural.

Phrygian

We can visit Phrygian on E from D. It has small then large intervals, noted as "SL":

Hijaz

New scale shape Hijaz (Phrygian sharp third). Note that the wide interval is a major third wide. It is so wide, that sometimes this major third might be cut in half into a pair of intervals. It could be: LS, SL, or MM. Using MM would be like Bayati on F!

Zamzama

Following from this position on F - SLS

Note that if rooted on note 1, it's the harmonic minor tetrachord.

Saba

Following from this position on F - MMS

Rast

Rast is a comon major-like scale (more like Dorian quartersharp minor third). The root note is 0, but there is strong emphasis on 1 and 4. If 1 were the center, it would be Bayati. Notice the pattern of notes creeping up one fret per string. This is useful for visualizing fretboard location

Now, go to Maqam World and read about Ajnas

Generic Shape

More generally, the pentatonic core is stable; and other notes tend to move around to suit the circumstances. Note that in none of this have you seen an actual quartertone (1 fret) interval. The harmonics on a string generally dictate where notes will lie, and there isn't a useful second interval much smaller than a half tone (2 fret - small step).

This is another generic shape that arises, which is roughly centered around a Rast tonality. This scale is practically impossible to resolve with non-quartertone instruments playing along though.

Harmonics

The reasoning behind the importance of interval sizes has to do with harmonics. Harmonic 1 is the full string, 2 is octave, etc. The importance in the order: octave, fifth, fourth, maj third, min third are made obvious by harmonics up to about 6. The more fine intervals get their importance from how well they evenly divide these intervals. This is why fret distances of 1 never appear in these scales. Small seconds intervals are somewhere from harmonic 18 to 15. Medium seconds intervals are somewhere from 13 to 11. Large seconds intervals are around 9 to 10.

Notice that harmonic 5 is slightly flat of the nearby fret. This is why when playing a maj third interval between two strings, bend the bottom note up a little bit until the timbre of the chord cleans up (and the beating goes away). This narrows the distance between the two notes.

Similarly harmonic 6 is slightly sharp of the nearby fret. So when playing minor third intervals between two strings, bend the top note up a little bit until the timbre of the chord cleans up (again, eliminates beating). This stretches the distance between the two notes.

Other intervals like a semitone (ie: an E and F played together) can be made just by bending the F up a little bit to clean up the chord. The locations of the harmonics make it clear what the pattern of adjustments for intervals is going to be.

53 Equal Temperment

In books on Maqam, the topic of alternate equal temperments as landmarks comes up. After 24 equal as a useful approximation (for notating notes especially), 53 equal arises as a way to accurately reason about the microtonal details. (See Touma's book "Music Of The Arabs").

Maqam is closely tied to Pythagorean tuning, where scales can be roughly thought of as a span of perfect fifths. A span of 53 perfect fifths comes so close to closing into a circle, that as far as this drawing goes, it doesn't matter whether we literally draw a scale created by spanning 53 perfect fifths or using 53 equal temperment. See how well the more important harmonics line up with fret locations.

The fret widths drawn were automatically generated based on how close they are in the perfect circle of fifths. Many instruments only include a subset of these frets, using a span of 22 fifths. That leaves a pattern where whole tones are cut into 9 equal parts, where whole tones (from fret 0 to fret 9, a pitch difference of 9/8) have no exact semitone. There is a semitone at either 4 or 5, for high or low semitones. Usually, the large semitone is used, as it more closely matches actual harmonics. When moving from note to note, there are temporary chords of a semitone going on.

In this system:

• A fifth is 31 frets
• A fourth is 22 frets (and is how we tune the strings to each other)
• A large whole tone is 9 frets, corresponding to 9/8 pitch.
• A small whole tone is 8 frets, corresponding to 10/9 pitch.
• The harmonic series says that a minor third is fret 14 for 6/5 pitch.
• But by perfect circle of fifths (ie: Pythagorean reasoning), a minor third is fret 13, corresponding to (4/3)^3 (ie: if you tune a guitar with harmonics E A D G, G will be (4/3)^3.
• Similarly, the choice of major third by harmonics pitch 5/4. That matches fret 17 quite closely. But by Pythagorean reasoning, this is two whole tones up to fret 18, reached by (3/2)^4.
• In both cases, the ratio 81/80 makes the difference between harmonics and Pythagorean reasoning.
• In spite of Maqam being strongly oriented around quartertone intervals, the best choice for a quartertone is 13/12. In practice, 11/10 is usually what is meant by a quartertone, but it doesn't quite match a 53et fret. Sometimes 12/11 is meant (in between 13/12 and 11/10), but it also isn't quite accurately represented by a 53equal fret. (It happens to be that the 24et quartertone is basically a 12/11.) In this case though, if notes are notated in 53et with a qualification that the note is a little low or high, there can be very little doubt as to exactly what pitch is implied.

When reading ambiguous statements like, "the major third of Ajam needs to be lowered a little bit to be more mellow", the reasoning behind it is much more obvious when the fretboard is at least thought of in terms of 53 equal temperment. In that case, the idea is to make the major third match 5/4.

As a side-note about a common definition of "Sruti", a span of 22 perfect fifths will cause a scale that is very close to 12et to arise; except every note other than the root and fifth will have a doubled partner very close by (roughly distance 81/80 away). Similarly, a span of 17 perfect fifths gives a Pythagorean intonation where sharps and flats are distinct, like split black keys. Then spanning only 12 gives the true Pythagorean piano tuning, with its wolf interval among an otherwise fantastic intonation. Spanning 7 gives a purely intoned diatonic scale, and spanning 5 gives a purely intoned pentatonic scale.

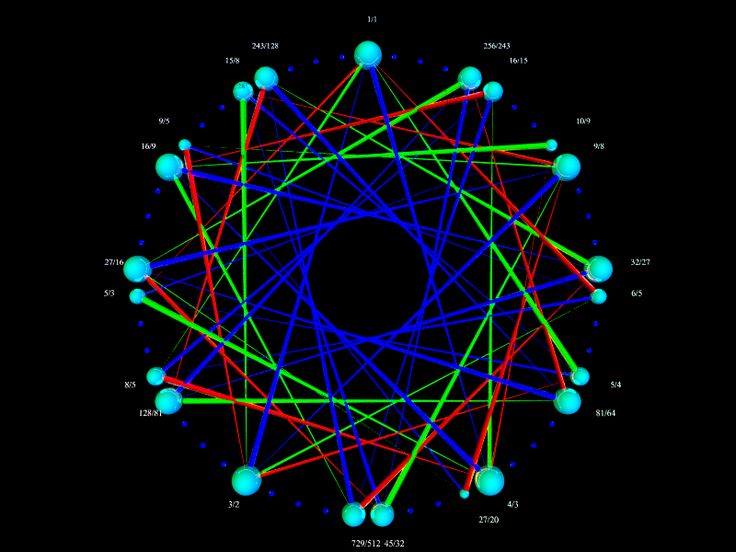
Using this diagram, you can calculate explicitly how to reach a 53et fret by navigating in terms of only fourths, fifths, maj third, min third. The given ratios are just the more obvious equivalent ratios at that location. The point of this diagram is to show that 12et is an approximation of this Sruti span of 22 perfect fifths. And even though it's defined in terms of "3-limit" (pure fifths), it actually contains some "5-limit" (including Just Intonation thirds). And finally, the 53 equal temperment encompasses them both. To some degree, this whole system exists as a side-effect of people playing string instruments with the strings tuned fourths and fifths apart; where the 81/80 pitch drift depending on melodic path is an issue that must be explicitly dealt with. 12et simply equates these close note pairs to make them go away in theory, but this issue still exists physically in the sound; creating a tension between clean chorde timbre (ie: beating) versus having distinct instruments playing from the same pitch set.

Other equal temperments are possible. For practical reasons, 31 equal temperment might be a reasonable upper limit for most fretted and keyed instruments. Just for the sake of completeness, I will include it here. It is well known for being a great choice for triads (major and minor chords). It also doesn't have the 81/80 problem, as it is theoretically derived from a Just circle of major thirds. But note that it's not a great fit for Pythagorean intervals, which is important to support in maqam.

The important pitch ratios are in this (large) image as an octave equivalent ratio oriented pitch wheel.

Suggestions

Based on this, materials and price issues aside, it may be ideal in a microtonal guitar (fretted or unfretted) to:

• For quartertone guitars, perhaps fret coloring or width should alternate for even and odd frets. Or maybe this should be part of the inlay pattern. The Kamal Musallam Ibanez Oriental Series actually does this, though it isn't fully quartertone fretted, even at the bottom of the neck.
• If a subset of 53 equal temperment can't be used, then perhaps fretless necks should be inlaid with a 53 equal temperment pattern. This pattern should roughly look like the 53EDO diagram to make it easy to visually count out the long fret jumps. Playing an actual 53 equal temperment guitar will require having a fretboard vision that quickly locates wholetone, fourth, and fifth relationships. GeoSynthesizer has such a pattern, but that pattern relies on "flattening" out the distance between frets so that lines can be drawn between strings that make it easy to intuitively play Just Intonation chords even with comma drift happening. (Comma drift is landing one fret off at the end of navigating a phrase by pure pitch ratios.)